DILATAÇÃO,  ENTROPIA E ENTALPIA QUÂNTICA [S] NO GRACELI NO SDCITE GRACELI

TERCEIRA QUANTIZAÇÃO PELO SDCTIE GRACELI

TRANS-QUÂNTICA SDCTIE GRACELI, TRANSCENDENTE, RELATIVISTA SDCTIE GRACELI, E TRANS-INDETERMINADA.

FUNDAMENTA-SE EM QUE TODA FORMA DE REALIDADE SE ENCONTRA EM TRANSFORMAÇÕES, INTERAÇÕES, TRANSIÇÕES DE ESTADOS [ESTADOS DE GRACELI], ENERGIAS E FENÔMENOS DENTRO DE UM SISTEMA DE DEZ OU MAIS DIMENSÕES DE GRACELI, E CATEGORIAS DE GRACELI.

FUNÇÃO GERAL GRACELI DA TRANS- INDETERMINALIDADE PELO SDCTIE GRACELI

FUNÇÃO FUNDAMENTAL E GERAL DO SISTEMA [SDCTIE GRACELI] DE  INTERAÇÕES, TRANSFORMAÇÕES EM CADEIAS, DECADIMENSIONAL E CATEGORIAL GRACELI.  E DE ESTADOS TRANSICIONAIS =

TRANSFORMAÇÕES ⇔ INTERAÇÕES  ⇔  TUNELAMENTO ⇔ EMARANHAMENTO ⇔ CONDUTIVIDADE  ⇔ DIFRAÇÕES ⇔ estrutura eletrônica, spin, radioatividade, ABSORÇÕES E EMISSÕES INTERNA ⇔  Δ de temperatura e dinâmicas, transições de estados quântico Δ ENERGIAS,  ⇔   Δ MASSA ,   ⇔ Δ  CAMADAS ORBITAIS ,  ⇔  Δ FENÔMENOS  ,  ⇔  Δ  DINÂMICAS,   ⇔  Δ  VALÊNCIAS,   ⇔  Δ BANDAS,  Δ  entropia e de entalpia,  E OUTROS.  

x

 [EQUAÇÃO DE DIRAC].

 + FUNÇÃO TÉRMICA.

   +    FUNÇÃO DE RADIOATIVIDADE

  ,      +   FUNÇÃO DE TUNELAMENTO QUÂNTICO.

  + ENTROPIA REVERSÍVEL 

+      FUNÇÃO DE CONDUÇÃO ELETROMAGNÉTICA

 ENERGIA DE PLANCK

X

• 
  V [R] [MA] =  Δe,M, Δf, ΔE, Δt, Δi, ΔT, ΔC, ΔE,ΔA, ΔD, ΔM......

  ΤDCG

  X

  Δe, ΔM, Δf, ΔE, Δt, Δi, ΔT, ΔC, ΔE,ΔA, ΔD, ΔM......  =
  x
  

  sistema de dez dimensões de Graceli + 

  DIMENSÕES EXTRAS DO SISTEMA DECADIMENSIONAL E CATEGORIAL GRACELI.[como, spins, posicionamento, afastamento, ESTRUTURA ELETRÔNICA, e outras já relacionadas]..
• 
  
• DIMENSÕES DE FASES DE ESTADOS DE TRANSIÇÕES DE GRACELI.
  

  x

  sistema de transições de estados, e estados  de Graceli, fluxos aleatórios quântico, potencial entrópico e de entalpia. [estados de transições de fases de estados de estruturas, quântico, fenomênico, de energias, e dimensional [sistema de estados de Graceli].

  x

número atômico, estrutura eletrônica, níveis de energia 

[comprimento de onda (λ).

onde c, velocidade da luz, é igual a .]

X

• TEMPO ESPECÍFICO E FENOMÊNICO DE GRACELI.
• X
• CATEGORIAS DE GRACELI
• T l    T l     E l       Fl         dfG l   

  N l    El                 tf l

  P l    Ml                 tfefel 

  Ta l   Rl

           Ll
           D

X

 [ESTADO QUÂNTICO]

X

TODA FORMA DE FUNÇÃO E EQUAÇÃO EM:

Em 1929, o físico Oskar Klein^[1] obteve um resultado surpreendente através da aplicação da equação de Dirac para o problema familiar de espalhamento de elétrons por uma barreira de potecial. Na mecânica quântica não-relativística, o tunelamento de elétrons em uma barreira é observado, com amortecimento exponencial. No entanto, o resultado de Klein mostrou que, se o potencial é da ordem da massa do elétron, ${\displaystyle V\sim mc^{2}}$, a barreira é quase transparente. Além disso, conforme o potencial se aproxima do infinito, a reflexão diminui e o elétron é sempre transmitido.

A aplicação imediata do paradoxo foi o modelo próton-elétron de Rutherford para partículas neutras dentro do núcleo, antes da descoberta do nêutron. O paradoxo apresentou uma objeção quântica com a noção de um elétron confinado dentro de um núcleo.^[2] Este paradoxo claro e preciso sugeriu que um elétron não pode ser confinado dentro de um núcleo por qualquer poço de potencial. O significado desse paradoxo foi intensamente debatida na ocasião.^[2]

Partículas sem massa[editar | editar código-fonte]

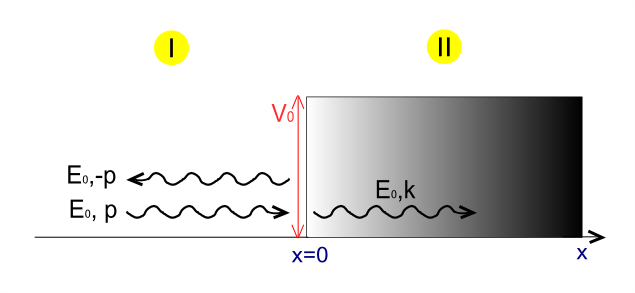
Considere uma partícula sem massa relativistica se aproximando de um potencial degrau de altura ${\displaystyle V_{0}}$ com energia ${\displaystyle E_{0}<V_{0}}$ e momento ${\displaystyle p}$.

A função de onda da partícula, ${\displaystyle \psi }$, segue a equação de Dirac independente do tempo:

${\displaystyle \left(\sigma _{x}p+V\right)\psi =E_{0}\psi ,\quad V={\begin{cases}0,&x<0\\V_{0},&x>0\end{cases}}}$

E ${\displaystyle \sigma _{x}}$ é a matriz de Pauli:

${\displaystyle \sigma _{x}=\left({\begin{matrix}0&1\\1&0\end{matrix}}\right)}$

Fig. 1 Descrição da relação de dispersão, o eixo x representa o momento enquanto que o eixo y representa a energia.

Assumindo que a partícula está se propagando a partir da esquerda, obtemos duas soluções — um antes do degrau, na região (1) e um abaixo do potencial, na região (2):

${\displaystyle \psi _{1}=Ae^{ipx}\left({\begin{matrix}1\\1\end{matrix}}\right)+A'e^{-ipx}\left({\begin{matrix}-1\\1\end{matrix}}\right),\quad p=E_{0}\,}$

${\displaystyle \psi _{2}=Be^{ikx}\left({\begin{matrix}1\\1\end{matrix}}\right),\quad \left|k\right|=V_{0}-E_{0}\,}$

Onde os coeficientes A, A′ e B são números complexos. Ambas as funções de onda incidente e transmitida estão associados com velocidade de grupo positiva (Linhas azuis na Fig.1), enquanto que a função de onda refletida é associado com velocidade de grupo negativa. (Linhas verdes na Fig.1)

Agora queremos calcular os coeficientes de transmissão e reflexão, ${\displaystyle T,R.}$ Eles são derivados da correntes de amplitude de probabilidade.

A definição da corrente de probabilidade associada com a equação de Dirac é:

${\displaystyle J_{i}=\psi _{i}^{\dagger }\sigma _{x}\psi _{i},\ i=1,2\,}$

Nesse caso:

${\displaystyle J_{1}=2\left[\left|A\right|^{2}-\left|A'\right|^{2}\right],\quad J_{2}=2\left|B\right|^{2}\,}$

Os coeficientes de transmissão e reflexão são:

${\displaystyle R={\frac {\left|A'\right|^{2}}{\left|A\right|^{2}}},\quad T={\frac {\left|B\right|^{2}}{\left|A\right|^{2}}}\,}$

A continuidade da função de onda em ${\displaystyle x=0}$, nos fornece:

${\displaystyle \left|A\right|^{2}=\left|B\right|^{2}\,}$

${\displaystyle \left|A'\right|^{2}=0\,}$

E assim, o coeficiente de transmissão é 1 e não há reflexão.

Uma interpretação do paradoxo é de que um potencial degrau não pode inverter a direção da velocidade de grupo de uma partícula relativística sem massa. Esta explicação se adéqua melhor a solução de partícula única citada acima. Interpretações mais complexas são sugeridas na literatura, no contexto da teoria quântica de campos onde é mostrado que o tunelamento desenfreado ocorre devido à existência de pares de partículas-antipartícula no potencial.

Na mecânica quântica, equação de Dirac é uma equação de onda relativística proposta por Paul Dirac em 1928 que descreve com sucesso partículas elementares de spin-½, como o elétron. Anteriormente, a equação de Klein-Gordon (uma equação de segunda ordem nas derivadas temporais e espaciais) foi proposta para a mesma função, mas apresentou severos problemas na definição de densidade de probabilidade. A equação de Dirac é uma equação de primeira ordem, o que eliminou este tipo de problema. Além disso, a equação de Dirac introduziu teoricamente o conceito de antipartícula, confirmado experimentalmente pela descoberta em 1932 do pósitron, e mostrou que spin poderia ser deduzido facilmente da equação, ao invés de postulado. Contudo, a equação de Dirac não é perfeitamente compatível com a teoria da relatividade, pois não prevê a criação e destruição de partículas, algo que apenas uma teoria quântica de campos poderia tratar.

A equação propriamente dita é dada por:

${\displaystyle \left(\alpha _{0}mc^{2}+\sum _{j=1}^{3}\alpha _{j}p_{j}\,c\right)\psi (\mathbf {x} ,t)=i\hbar {\frac {\partial \psi }{\partial t}}(\mathbf {x} ,t)}$,

na qual m é a massa de repouso do elétron, c é a velocidade da luz, p é o operador momentum linear ${\displaystyle \hbar }$ é a constante de Planck divida por 2π, x e t são as coordenadas de espaço e tempo e ψ(x, t) é uma função de onda com quatro componentes.

Cada α é um operador linear que se aplica à função de onda. Escritos como matrizes 4×4, são conhecidos como matrizes de Dirac. Uma das escolhas possíveis de matrizes é a seguinte:

${\displaystyle \alpha _{0}={\begin{bmatrix}1&0&0&0\\0&1&0&0\\0&0&-1&0\\0&0&0&-1\end{bmatrix}}\quad \alpha _{1}={\begin{bmatrix}0&0&0&1\\0&0&1&0\\0&1&0&0\\1&0&0&0\end{bmatrix}}}$

${\displaystyle \alpha _{2}={\begin{bmatrix}0&0&0&-i\\0&0&i&0\\0&-i&0&0\\i&0&0&0\end{bmatrix}}\quad \alpha _{3}={\begin{bmatrix}0&0&1&0\\0&0&0&-1\\1&0&0&0\\0&-1&0&0\end{bmatrix}}}$.

Na mecânica quântica, o caso de uma partícula em um anel unidimensional é semelhante à partícula em uma caixa^[1][2]. A equação de Schrödinger para uma partícula livre que é restrita a um anel^[3] (tecnicamente, cujo espaço de configuração é o círculo ${\displaystyle S^{1}}$) é

${\displaystyle -{\frac {\hbar ^{2}}{2m}}\nabla ^{2}\psi =E\psi }$

Função de onda[editar | editar código-fonte]

Usando coordenadas polares no anel unidimensional de raio R, a função de onda depende somente da coordenada angular, e assim

${\displaystyle \nabla ^{2}={\frac {1}{R^{2}}}{\frac {\partial ^{2}}{\partial \theta ^{2}}}}$

exigindo que a função de onda seja periódica em ${\displaystyle \ \theta }$ com um período ${\displaystyle 2\pi }$ (da demanda de que as funções de onda sejam funções de valor único no círculo), e que elas sejam normalizadas leva às condições

${\displaystyle \int _{0}^{2\pi }\left|\psi (\theta )\right|^{2}\,Rd\theta =1\ }$,

e

${\displaystyle \ \psi (\theta )=\ \psi (\theta +2\pi )}$

Nestas condições, a solução da equação de Schrödinger é dada por

${\displaystyle \psi _{\pm }(\theta )={\frac {1}{\sqrt {2\pi R}}}\,e^{\pm i{\frac {R}{\hbar }}{\sqrt {2mE}}\theta }}$

Um problema importante na mecânica quântica é o de uma partícula num potencial esfericamente simétrico, isto é, um potencial que depende apenas da distância entre a partícula e um ponto central definido. Em particular, se a partícula em questão é um elétron e o potencial é derivado da lei de Coulomb, então o problema pode ser usado para descrever um átomo de hidrogênio (um elétron ou íon).

No caso geral, a dinâmica de uma partícula em um potencial esfericamente simétrico é governada por um hamiltoniano da seguinte forma:

${\displaystyle {\hat {H}}={\frac {{\hat {p}}^{2}}{2m_{0}}}+V(r)}$

onde ${\displaystyle m_{0}}$ é a massa da partícula, ${\displaystyle {\hat {p}}}$ é o operador momentum, e o potencial ${\displaystyle V(r)}$ depende apenas de ${\displaystyle r}$, o módulo do vetor raio; r. As funções e energias da onda quântica (autovalores) são encontradas resolvendo a equação de Schrödinger com este hamiltoniano. Devido à simetria esférica do sistema, é natural usar coordenadas esféricas ${\displaystyle r}$, ${\displaystyle \theta }$ e ${\displaystyle \phi }$. Quando isso é feito, a equação de Schrödinger independente do tempo para o sistema é separável, permitindo que os problemas angulares sejam tratados facilmente, e deixando uma equação diferencial ordinária em ${\displaystyle r}$ para determinar as energias para o potencial particular ${\displaystyle V(r)}$ em discussão.

Descrição quântica do problema[editar | editar código-fonte]

O problema pode apresentar-se em qualquer número de dimensões, mas o mais simples é o problema unidimensional, ainda que o mais útil é o que se centra em uma caixa tridimensional. Em uma dimensão, se representa por uma partícula que existe em um segmento de uma linha, sendo as paredes os pontos finais do segmento.

Em termos da física, a partícula em uma caixa se define como uma partícula pontual, encerrada em uma caixa onde não experimenta nenhum tipo de força (ou seja, sua energia potencial é constante, ainda que sem perda de generalidade podemos considerar que vale zero). Nas paredes da caixa, o potencial aumenta até um valor infinito, fazendo-a impenetrável. Usando esta descrição em termos de potenciais nos permite usar a equação de Schrödinger para determinar uma solução.

Esquema do potencial para a caixa unidimensional.

Como se menciona acima, se estivéssemos estudando o problema sob as regras da mecânica clássica, deveríamos aplicar as leis do movimento de Newton às condições iniciais, e o resultado seria razoável e intuitivo. Em mecânica quântica, quando se aplica a equação de Schrödinger, os resultados não são intuitivos. Em primeiro lugar, a partícula só pode ter certos níveis de energia específicos, e o nível zero não é um deles. Em segundo lugar, as probabilidades de detectar a partícula dentro da caixa em cada nível específico de energia não são uniformes - existem várias posições dentro da caixa onde a partícula pode ser encontrada, mas também há posições onde é impossível fazê-lo. Ambos resultados diferem da maneira usual na que percebemos o mundo, inclusive se estão fundamentados por princípios extensivamente verificados através de experimentos.

Caixa monodimensional[editar | editar código-fonte]

A versão mais precisa se dá na situação idealizada de uma "caixa monodimensional", na que a partícula de massa m pode ocupar qualquer posição no intervalo [0,L]. Para encontrar os possíveis estados estacionários é necessário aplicar a equação de Schrödinger independente do tempo em uma dimensão para o problema:

${\displaystyle -{\cfrac {\hbar ^{2}}{2m}}{\cfrac {\mathrm {d} ^{2}\psi (x)}{\mathrm {d} x^{2}}}=E\psi (x)}$ [1]

Considerando que o potencial é zero dentro da caixa e infinito fora, e observando que a função de onde se anula fora da caixa, temos as seguintes condições de contorno:

${\displaystyle 0<x<L}$

${\displaystyle {\begin{cases}\psi (0)=0\\\psi (L)=0\end{cases}}}$ [1a]

e onde

${\displaystyle \hbar }$ é a Constante reduzida de Planck,

${\displaystyle m\,}$ é a massa da partícula,

${\displaystyle \psi \left(x\right)\,}$ é a função de onda estacionária independente do tempo^[1] que queremos obter (funções próprias) e

${\displaystyle E\,}$ é a energia da partícula (valor próprio).

As funções próprias e valores próprios de uma partícula de massa m em uma caixa monodimensional de comprimento L são:

${\displaystyle \psi _{n}(x)={\sqrt {\frac {2}{L}}}\sin {\left({\frac {n\pi x}{L}}\right)},\qquad E_{n}={\frac {\hbar ^{2}\pi ^{2}}{2mL^{2}}}n^{2}={\frac {h^{2}}{8mL^{2}}}n^{2},\qquad {\mbox{com}}\ n=1,2,3,...}$ [1b]

Níveis de energia (linhas discontínuas) e funções de onda (linhas contínuas) da partícula em uma caixa monodimensional.

Note-se que só são possíveis os níveis de energia "quantizados". Além disso, como n não pode ser zero (ver mais adiante), o menor valor da energia tampouco pode sê-lo. Esta energia mínima se chama energia do ponto zero e se justifica em termos do princípio de incerteza. Devido a que a partícula se encontra restringida a mover-se em uma região finita, a variância da posição tem um limite superior (o comprimento da caixa, ${\displaystyle L}$). Assim, de acordo com o princípio de incerteza, a variância do momento da partícula não pode ser zero e, portanto, a partícula deve ter uma certa quantidade de energia que aumenta quando a longitude da caixa L diminui.

Dedução

Na física, uma partícula livre é uma partícula que, em certo sentido, não está vinculada por uma força externa, ou equivalentemente não está em uma região onde sua energia potencial varia. Na física clássica, isso significa que a partícula está presente em um espaço "sem campo". Na mecânica quântica, significa uma região de potencial uniforme, geralmente modulada para zero na região de interesse, uma vez que o potencial pode ser arbitrariamente arranjado para zero em qualquer ponto (o

u superfície em três dimensões) no espaço.

Descrição matemática[editar | editar código-fonte]

Partícula livre clássica[editar | editar código-fonte]

A partícula livre clássica é caracterizada simplesmente por uma velocidade fixa v. O momento linear é dado por

${\displaystyle \mathbf {p} =m\mathbf {v} }$

e a energia cinética, que é igual à energia total, é dada por

${\displaystyle E={\frac {1}{2}}mv^{2}={\frac {p^{2}}{2m}}}$

onde m é a massa da partícula e v é o vetor velocidade da partícula.

Partícula livre quântica[editar | editar código-fonte]

Uma partícula livre na mecânica quântica (não relativística) é descrita pela equação de Schrödinger livre:

${\displaystyle -{\frac {\hbar ^{2}}{2m}}\nabla ^{2}\ \psi (\mathbf {r} ,t)=i\hbar {\frac {\partial }{\partial t}}\psi (\mathbf {r} ,t)}$

onde ψ é a função de onda da partícula na posição r e tempo t. A solução para uma partícula com momento p ou vetor de onda k, na freqüência angular ω ou energia E, é dada pela onda plana complexa:

${\displaystyle \psi (\mathbf {r} ,t)=Ae^{i(\mathbf {k} \cdot \mathbf {r} -\omega t)}=Ae^{i(\mathbf {p} \cdot \mathbf {r} -Et)/\hbar }}$

com amplitude A. Como para todas as partículas quânticas livres ou ligadas, o princípio da incerteza de Heisenberg

${\displaystyle \Delta p_{x}\Delta x\geq {\frac {\hbar }{2}},\quad \Delta E\Delta t\geq \hbar }$

(da mesma forma para as direções y e z) e as relações De Broglie:^[1]:

${\displaystyle \mathbf {p} =\hbar \mathbf {k} ,\quad E=\hbar \omega }$

se aplicam. Como a energia potencial é adotada como zero, a energia total E é igual à energia cinética, que tem a mesma forma da física clássica:

${\displaystyle E=T\,\rightarrow \,{\frac {\hbar ^{2}k^{2}}{2m}}=\hbar \omega }$

Há várias equações que descrevem partículas relativísticas: veja equações de onda relativísticas.^[2][3][4][5]

Partículas idênticas e energia de intercâmbio[editar | editar código-fonte]

É possível elucidar estas afirmações com um pouco de detalhe técnico. A "identidade" das partículas está ligada à simetria dos estados mecanico-quânticos devido ao intercâmbio de etiquetas das partículas. Isto dá lugar a dois tipos de partículas, que se comportam de forma diferente, chamadas férmions e bósons. (Há também um terceiro tipo, anyons e sua generalização, pléktons).

Se considerarmos um sistema com duas partículas idênticas, pode-se supor que o vetor de estado de uma partícula é |ψ>, e o vetor de estado da outra partícula é |ψ′>. Pode-se representar o estado do sistema combinado, que é uma combinação não especificada dos estados de uma partícula, como:

${\displaystyle |\psi \psi ^{\prime }\rangle }$.

Se as partículas são idênticas, então: (i) seus vetores de estados ocupam espaços de Hilbert matematicamente idênticos; e (ii) |ψψ′> e |ψ′ ψ> terão a mesma probabilidade de colapsar a qualquer outro estado multipartícula |φ>:

${\displaystyle |\langle \phi |\psi \psi ^{\prime }\rangle |^{2}=|\langle \phi |\psi ^{\prime }\psi \rangle |^{2}}$

Esta propriedade se chama simetría de intercâmbio. Uma forma de satisfazer essa simetría é que a permutação só induza uma fase:

${\displaystyle |\psi \psi ^{\prime }\rangle =e^{i\alpha }|\psi ^{\prime }\psi \rangle }$

Sem dúvida, duas permutações conduzirão à identidade (visto que as etiquetas voltarão a suas posições originais), donde se requer que e^2iα = 1. Então, ou

${\displaystyle |\psi \psi ^{\prime }\rangle =+|\psi ^{\prime }\psi \rangle }$

que se chama um estado totalmente simétrico, ou

${\displaystyle |\psi \psi ^{\prime }\rangle =-|\psi ^{\prime }\psi \rangle }$

que se chama estado totalmente antisimétrico.

O pêndulo quântico é fundamental para entender as rotações internas impedidas na química, as características quânticas dos átomos de dispersão, bem como numerosos outros fenômenos quânticos.^[1] Embora um pêndulo não sujeito à aproximação de pequeno ângulo tenha uma não-linearidade inerente, a equação de Schrödinger para o sistema quantizado pode ser resolvida de forma relativamente fácil.^[2][3][4]

Equação de Schrödinger[editar | editar código-fonte]

Usando a teoria lagrangiana da mecânica clássica, pode-se desenvolver um hamiltoniano para o sistema. Um pêndulo simples tem uma coordenada generalizada (o deslocamento angular ${\displaystyle \phi }$) e duas restrições (o comprimento da corda e o plano de movimento). As energias cinéticas e potenciais do sistema podem ser encontradas em

${\displaystyle T={\frac {1}{2}}ml^{2}{\dot {\phi }}^{2},}$

${\displaystyle U=mgl(1-\cos \phi ).}$

Isso resulta no Hamiltoniano

${\displaystyle {\hat {H}}={\frac {{\hat {p}}^{2}}{2ml^{2}}}+mgl(1-\cos \phi ).}$

A equação de Schrödinger dependente do tempo para o sistema é

${\displaystyle i\hbar {\frac {d\Psi }{dt}}=-{\frac {\hbar ^{2}}{2ml^{2}}}{\frac {\mathrm {d} ^{2}\Psi }{\mathrm {d} \phi ^{2}}}+mgl(1-\cos \phi )\Psi .}$

É preciso resolver a equação de Schrödinger independente do tempo para encontrar os níveis de energia e os auto-estados correspondentes. Isso é efetuado melhor alterando a variável independente da seguinte maneira:

${\displaystyle \eta =\phi +\pi ,}$

${\displaystyle \Psi =\psi e^{-iEt/\hbar },}$

${\displaystyle E\psi =-{\frac {\hbar ^{2}}{2ml^{2}}}{\frac {\mathrm {d} ^{2}\psi }{\mathrm {d} \eta ^{2}}}+mgl(1+\cos \eta )\psi .}$

Esta é a equação de Mathieu.^[5]

${\displaystyle {\frac {\mathrm {d} ^{2}\psi }{\mathrm {d} \eta ^{2}}}+\left({\frac {2mEl^{2}}{\hbar ^{2}}}-{\frac {2m^{2}gl^{3}}{\hbar ^{2}}}-{\frac {2m^{2}gl^{3}}{\hbar ^{2}}}\cos \eta \right)\psi =0,}$

onde as soluções são as funções Mathieu.^[6][7][8]